Deep Gaussian Process models for Real-Time Blendshape Prediction on GPU
Research Area:
Biomedical and Biologically Motivated Technical ApplicationsResearchers:
Nick Taubert; Martin A. GieseDescription:
The superior generalization properties of GPs with limited training data have made Gaussian process models a popular choice for motion synthesis and editing techniques. The domain of computer graphics robotics have widely used Gaussian process latent variable models (GP-LVM) for kinematic modelling and motion interpolation, inverse kinematics, and learning of low-dimensional dynamical models.
Despite their advantages, Gaussian process models have limitations. Their high computational complexity makes many of these techniques unsuitable for embedding online control systems and resulting in offline models. Applying sparse approximation techniques to solve this issue for real-time applications and larger data sets can lead to overfitting. Although approximate inference in the form of variational free energy (VFE) framework can control overfitting, it has the drawback of producing unnecessarily large memory footprints during learning and is not parallelizable, making it unsuitable for GPU implementations.
Therefore, we propose approximate inference exploiting expectation propagation (EP) as a framework which is parallelizable during learning, produces more accurate approximations, and in form of Power EP combines the advantages of VFE and EP within a single algorithm and enables deep architectures in form of continuous deep neural networks.
Blendshape Inference
Initially, we developed an implementation of our technique as a plugin designed for Autodesk Maya, enabling real-time inference of blendshapes. This plugin serves the purpose of deriving facial expressions for virtual characters, utilizing input provided by users. By leveraging the GP plugin, individuals can animate the character by utilizing their own facial expressions captured through a webcam.
Blendshape animation based on user input.
During the training process, we employed a total of 43 controller inputs, each carefully aligned with 193 corresponding blendshapes. This meticulous matching ensured accurate mapping between the controller positions and the associated blendshapes. Notably, the entire workflow for asset preparation and model training was seamlessly integrated within Maya's node structure. As a result, there was no requirement for importing or exporting training data, streamlining the overall process and enhancing efficiency. The algorithm is implemented in C++ using stochastic Expectation Propagation for fast inference on GPU and enabling scalability for deep architectures of Gaussian Processes.
Learning of 43 controller with 193 position variations (based on blendshapes).
Expectation Propagation
EP is a deterministic algorithm used for Bayesian inference. Its purpose is to approximate joint-distributions that are factorizable but otherwise intractable. By evaluating the observed data, EP returns a tractable version of the joint-distribution. In GP regression, this approximation takes the form of an unnormalized process, where $q^*(f|\theta)$ approximates $p(\mathbf{y},f|\theta)$, with the superscript $*$ denoting unnormalized.
The main idea behind EP and other distributional inference approximations, such as Variational Free Enery (VFE) and Power EP, is to decompose the joint-distribution into relevant terms. Specifically, they aim to express $p(f, \mathbf{y}|\theta)=p^*(\mathbf{y}|f,\theta)=p(\mathbf{y}|\theta)p(f|\mathbf{y},\theta)$. These approximations are expressed in tractable terms of the decomposed form, where $q^*(f|\theta)=Zq(f|\theta)$ and the normalization constant $Z$ approximates the marginal likelihood $p(\mathbf{y}|\theta)$. The posterior is approximated by a GP sparse approximation, so that $p(f|\mathbf{y},\theta)\approx q(f|\theta)$. Therefore, the approximate inference schemes simultaneously provide unnormalized Gaussian process approximations of the posterior and marginal likelihood in the form of $q^*(f|\theta)$.
Stochastic Expectation Propagation (SEP) reduces the memory complexity of Power EP by a factor of $N$ by parameterizing a global factor that captures the average effect of a likelihood on the posterior. The approximate posterior set can be rewritten as $p^*(f|\mathbf{y},\theta)=p(f|\theta)t(\mathbf{u})^N$, where $t(\mathbf{u})^N$ is the global approximation factor. SEP combines the benefits of local and global approximation, making it tractable, distributable, and parallelizable while reducing memory demands. The set of the approximate posterior can be rewritten as,
![]()
One approach is to use the iterative process of Power EP to compute approximate factorizations, and then optimize hyperparameters in an outer loop also using Power EP. However, using a factor tying approximation, the optimization problem can be simplified into a minimization problem. This means that the approximate Power EP energy can be optimized using standard optimization algorithms such as ADAM or L-BFGS-B, allowing for simultaneous optimization of both the approximate posterior and hyperparameters at each iteration step.
Implementation in Unreal Engine 5
Thanks to our C++ implementation, our algorithm can be seamlessly integrated into Unreal Engine's node structure, offering the advantage of setting up scene logic through blueprints. Unreal Engine's graphical programming interface empowers users to accomplish tasks without the need for extensive programming skills. By leveraging the GP node within the blueprint system, users gain the ability to interact with all built-in nodes, enabling the creation of customized logic to suit their specific requirements. This integration opens up a wide range of possibilities for users to efficiently and creatively develop their desired scene logic within the Unreal Engine environment.
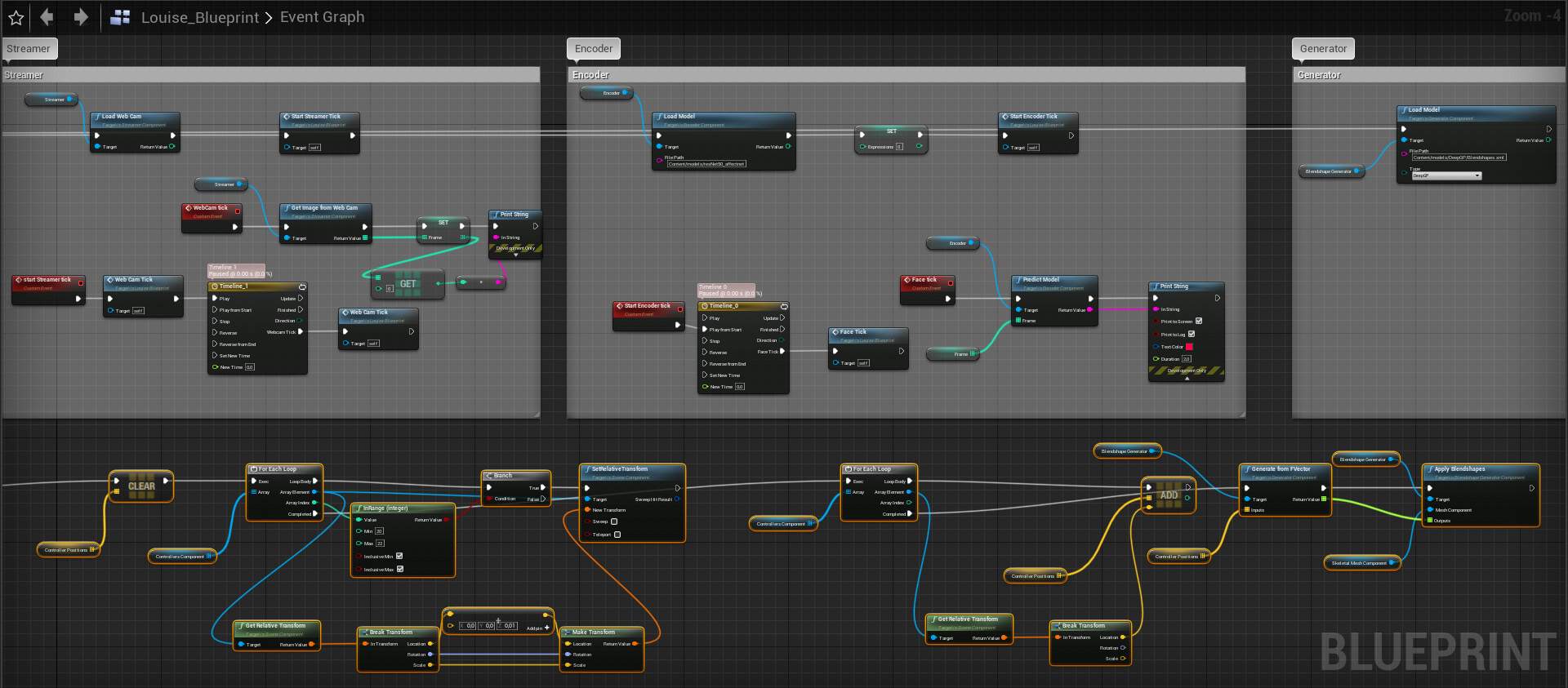
Blueprint implementation of Deep GP for blendshape inference.
During our experiments involving real monkeys, we substituted the human character with a virtual monkey head. By analyzing the facial expressions of a real human, we accurately derived the most probable blendshapes for the virtual monkey head. Notably, the rendering process was entirely conducted in real-time, despite the computationally demanding nature of fur rendering in Unreal Engine. This achievement showcases the efficiency and effectiveness of our approach, as we were able to maintain real-time rendering capabilities even with the resource-intensive fur rendering techniques employed within the Unreal Engine framework.
Real-time inference in Unreal Engine.
