Online motion synthesis by networks of learned dynamic primitives for humanoid robots
Research Area:
Biomedical and Biologically Motivated Technical ApplicationsResearchers:
Albert Mukovskiy; Martin A. GieseDescription:
Sequential goal-directed full-body motion is a challenging task for humanoid robots. An example is the coordination of bipedal walking with fast upper body movements. The figure shows reaching while walking. In humans this task is solved by a highly predictive coordination of walking and reaching, where the walking behaviour is adapted to the goal of the reaching already multiple steps before object contact, maximizing the comfort during the final reaching movements [Land et al., 2013]. The realization of such behaviors in humanoid robots is highly challenging since it requires the coordination of periodic as well as non-periodic movements combined with a control of dynamic balance.
Whole body movements of humans and animals are organized in terms of muscle synergies or movement primitives e.g. [Bernstein 1967, Flash and Hochner 2005, D’Avella and Bizzi 2005]. Such primitives characterize the coordinated involvement of subsets of the available degrees of freedom in different actions. The same applies to reaching while walking, where behavioral studies reveal a mutual coupling between the walking and the reaching components [Carnahan et al. 1996, Chiovetto and Giese 2013, Marteniuk and Bertram 2001]. The realism and human-likeness of synthesized movements in robotics and computer graphics can be improved by taking such biological constraints into account [e.g. Fod et al. 2002, Safonova et al. 2004].

Human reaching for a goal object in a drawer during walking; intermediate postures (normal walking step, step with initiation of reaching, standing while opening the drawer, and object reaching).
Video link: https://goo.gl/5HKiG7
To implement this idea in the context of a humanoid robot system we first learned movement components or synergies from kinematic data from humans and transferred those into an architecture that consists of coupled dynamical systems (dynamic movement primitives) that can be embedded in control architectures. We learn kinematic primitives from data sets of human motion applying blind source separation techniques [D’Avella and Bizzi 2005], where we found that anechoic mixture models lead to particularly compact representations [Omlor and Giese 2007, 2011; Chiovetto et al. 2013; 2016].
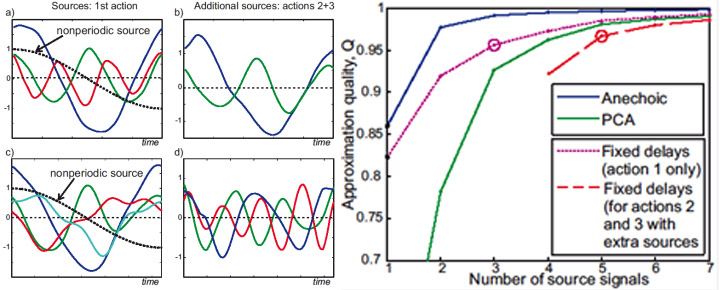
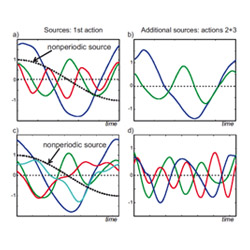
Left: Source signals (kinematic primitives) extracted by the anechoic de-mixing algorithm from the above coordinative task that combines walking with reaching for an object in a drawer, for different total number of extracted sources. Sources were extracted using a stepwise regression procedure (see Mukosvkiy et al. 2017b for details). Right: Comparison of approximation quality for different methods for blind source separation as function of the number of sources. (See Mukovskiy et al. 2017b for details).
The learned sets of kinematic primitives (source signals) reflect the structure of the task. One source is non-periodic and mainly affects the arm movement, reflecting the reaching movement and associated posture changes. The other sources mainly affect the walking component and differences between the individual steps before the final reaching step. The stepwise regression approach first fits the first step, and then adds additional sources for the following steps that capture differences between the step. A very good approximation of the human behaviour can be accomplished with only 6 sources.
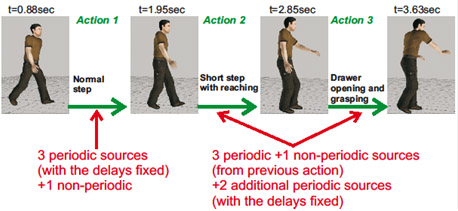
Stepwise regression procedure for the fitting of the source functions to the individual steps of the drawer scenario.
In order to generate such coordinated behaviors in real-time, and highly adaptively dependent on the boundary conditions of the task, we map the learned primitives onto a set of dynamical systems (dynamic primitives), which generate the source functions as solutions of nonlinear dynamical systems. These systems can be dynamically coupled to ensure the coordination of the different synergies or components that contribute to the behaviour. The underlying architecture is illustrated in the figure below. We can design systematically networks of coupled dynamic primitives with guaranteed stability properties exploiting methods from Contraction theory. (See [Mukovskiy et al. 2013] for details.) Such networks of dynamical primitives are basically nonlinear dynamical systems that can be embedded in control architectures of humanoid robots. We are able to generate online highly complex full-body motion as result of a self-organization process of dynamically coupled dynamic movement primitives. Such behaviour can adapt automatically to strong changes in the task space, such as the drawer jumping away during the reaching, requiring additional corrective steps for successful reaching, as illustrated in the figure below.
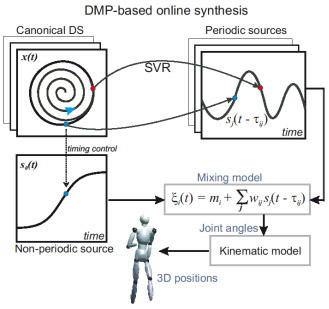
Mapping of kinematic primitives onto dynamic movement primitives. The source functions are generated in real-time as solutions of nonlinear dynamical systems, where a mapping between the state space of such systems and the source signal is established by Support Vector Regression (SVR). The joint angle trajectories are computed from the source functions by the learned anechoic mixture model. (See Mukovskiy et al. 2017a for details.).
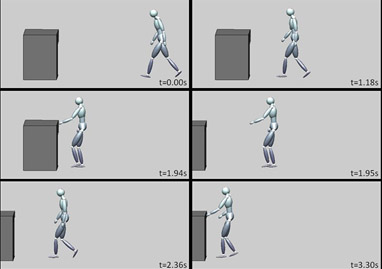
Online perturbation experiment. Here the drawer jumps away while the agent approaches by a large distance so that it can no longer be reached with the originally planned number of steps. The online planning algorithm adapts to this situation by introducing an additional step so that the behavior is successfully accomplished. The behavior has a very natural appearance even though this scenario was not part of the training data set.
Video link: https://goo.gl/EzTpsh
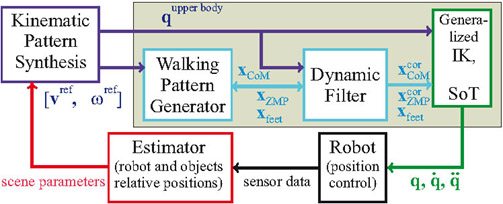
Control system for the humanoid robot HRP-2. The Walking Pattern Generator computes foot positions and CoM and ZMP trajectories, which are further adjusted by the Dynamic Filter, depending on the planned upper body motion. The resulting trajectories are consistent with the dynamic stability constraints of the robot. The module ‘Kinematic pattern Synthesis’ is formed by our architecture for the online synthesis of coordinated behaviors based on dynamic movement primitives (see above).
The described architecture for the online synthesis of reaching while walking was integrated, in collaboration with the CNRS-LAAS (Toulouse) in control architecture for the humanoid robot HRP-2. The developed online synthesis algorithm is used to plan online a (largely) robot-compatible behavioural strategy, which is the online corrected in order to ensure dynamic balance of the robot using a Stack-of-Task approach (architecture see figure below). In this way, complex coordinated behaviors can be realized, while guaranteeing that the robot does not fall down. See Mukovskiy et al. 2017b for details. The simulation in the figure below shows the automatic adjustment to a scenario where the drawer jumps away during reaching, taking into account the whole physics of the robot. The other figure below show the realization of the reaching behaviour (using a drawer distance that was not present in the training data) for the real humanoid robot at
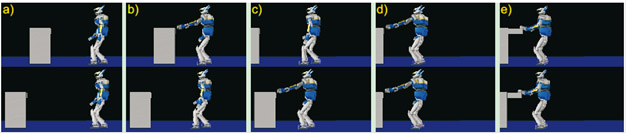
Realization of highly adaptive behaviour of reaching while walking, when the drawer jumps away during the approaching behaviour, using our architecture and simulating the full physics of the humanoid using the OpenHRP simulator. drawer in the upper row jumps to its new position. c) Drawer jumps to new position; d) final reach with the left arm; e) reaching for object inside drawer with the right hand.
Video link: https://goo.gl/upHLsx
Present work transfers the same approach for applications using a humanoid robot CoMan for rehabilitation training in cerebellar ataxia patients, exploiting a catching-throwing game. See Kodl et al. 2017, 2018; Mohammadi, et al. 2018 for further details.

Real HRP-2 robot performing a 4-action walking-reaching sequence in the robotics laboratory of LAAS/CNRS (Toulouse).
Video link: https://goo.gl/RqT6Q3
Acknowledgements: EC FP7 grant agreements: FP7-ICT-248311 “AMARSi”, FP7-ICT-611909 “Koroibot”; Horizon 2020 robotics program ICT-23-2014 grant agreement: 644727 – “CogIMon”.
External references:
[Bernstein 1967] Bernstein, N. A. (1967). The Coordination and Regulation of Movements. Pergamon Press, N.Y., Oxford, 1967.
[Carnahan et al 1996] Carnahan, H., McFadyen, B. J., Cockell, D. L. & Halverson, A. H. (1996). The combined control of locomotion and prehension. Neurosci. Res. Comm., 19:91–100.
[d’Avella and Bizzi 2005] d’Avella, A. & Bizzi, E. (2005). Shared and specific muscle synergies in neural motor behaviours. Proc. Natl. Acad. Sci. USA, 102(8):3076–3081.
[Flash and Hochner 2005] Flash, T. & Hochner, B. (2005). Motor primitives in vertebrates and invertebrates. Curr. Opin. Neurobiol., 15(6):660–666.
[Fod, et al. 2002] Fod, A., Mataric, M. J. & Jenkins O. C. (2002). Automated derivation of primitives for movement classification. Autonomous Robots, 12(1):39–54.
[Land, et al. 2013] Land, W. M., Rosenbaum, D. A., Seegelke, S. & Schack, T. (2013) Whole-body posture planning in anticipation of a manual prehension task: Prospective and retrospective effects. Acta Psychologica, 114:298–307.
[Marteniuk and Bertram 2001] Marteniuk, R. G. & Bertram, C. P. (2001). Contributions of gait and trunk movement to prehension: Perspectives from world- and body centered coordinates. Motor Control, 5:151–164.
[Safonova, et al. 2004] Safonova, A., Hodgins, J. & Pollard, N. (2004). Synthesizing physically realistic human motion in low-dimensional, behavior-specific spaces. ACM Trans. on Graphics, 23(3): 514–521.
