Online Controllable Models of Complex Body Movements for Biomedical Applications

Research Area:
Biomedical and Biologically Motivated Technical ApplicationsResearchers:
Jesse St-Amand; Winfried Ilg; Martin A. Giese; Alessandro Salatiello; Nick TaubertDescription:
Neural robotic control represents a promising approach to improving the autonomy and the quality of life for people with motor control disabilities, like those derived from spinal cord injury and stroke. This project aims towards the development of novel machine learning solutions for intuitive control of hand and arm rehabilitation devices (e.g. exoskeletons and prostheses).
Gaussian Process Latent Variable and Dynamical Models
For many applications, complex body movements are represented by machine learning methods. In biomedical applications and neuroprosthetics often only very limited amounts of training data are available, and also typically only a limited subset of activities has to be modeled with high accuracy, e.g. for control applications. Gaussian Process Latent Variable Models (GPLVMs) and Gaussian process Dynamical Models (GPDMs) turn out to allow the learning of highly accurate generative models of body movements from small amounts of data, at the same time being suitable for an embedding in probabilistic architectures that allow the estimation of missing variables and parameters by Bayesian inference. We extend such architectures by learning mixtures of classes of different movements, allowing online inference and synthesis from small amounts of training data. An application of this technology is the generation of bimanual movements from partial kinematic or EMG data in patients with one-sided impairments. The generated movements can be used to support the control of orthotic devices for patients with unilateral impairments, e.g. after stroke. This work has emerged as part of the project KONSENS-NHE in the neurorobotics framework of the Baden-Württemberg Stiftung.
Hierarchical GPLVM/GPDM Package Extension
For the development of our new framework, we created an extension of the package GPy (https://sheffieldml.github.io/GPy/) that has been developed by the University of Sheffield, and which supports the application and development of machine learning algorithms based on Gaussian Processes. Our package extension enables, specifically, the construction of hierarchical GPLVMs and GPDMs in a node-based learning format. These GPDMs may be flexibly adapted to first or second order dynamics. We also added extensions to implement both sparse GPLVMs and GPDMs within the hierarchy to reduce the computational complexity of learning. Additionally, we have integrated a framework that enables the implementation of different forms of back-constraints, allowing for their flexible application to GPLVMs within hierarchical architectures. Furthermore, we have implemented a framework for the realization of mixtures of GPDMs and associated algorithms for inference and online prediction.
Mixtures of GPDMs
In many applications in motor control, a set of different movements has to be modeled with high accuracy, while the types of movements that are executed are limited. This applies, particularly, to applications for patients with strong motor deficits that typical execute a much smaller spectrum of different activities than healthy individuals. Learning such movement classes, while potentially also modeling patient-specific particularities, from very limited data is a problem that cannot be easily solved with standard neural network approaches that require large amounts of data. Data-efficient methods, such as standard GPLVMS and GPDMs, successfully learn such models from limited data, but they have the disadvantage in providing accurate approximations for individual movement classes, but not for embedding distinct classes of movements within the same model. Learning multiple such classes of movements with the same model typically results in uncontrolled switching between different movement types.
Our solution to this problem was to include multiple GPDMs within the same latent space, wherein each GPDM learns a subset of the data defining a distinct action class. This prevents the dynamics of different actions from uncontrolled mixing, while still maintaining a framework that allows for accurate modeling of the trajectories from very limited data. The key for the development of such a mixture model was to establish the right trade-off between the clustering of body poses by the GM-LVM and the clustering by temporal continuity along the trajectories as implemented by the corresponding GPDM. As a result, we are able to learn classes of different actions with high approximation quality, all embedded within the same latent space, and while avoiding uncontrolled interpolations between different actions.
Back-Constraints
In its standard formulation, the GPLVM ensures a smooth mapping from the latent space to the data space, but does not ensure smoothness in the other direction. As such, the GPLVM will form a space wherein nearby latent points map to similar poses in the data, but it does not guarantee that similar poses in the data space will map to similar latent points. Back-constraints were designed for rectifying this problem, constraining the latent space to a smooth function of the data space. Many different functions can be used to define back-constraints. Common applications include non-linear kernel mappings and mappings that apply specific geometries, e.g., incorporating sin and cos in the mapping to impose a circular geometry on the space.
Due to the conflicting elements of the GPLVM and the GPDM prior’s likelihood function contributions (see section Mixtures of GPDMs), a mixture of GPDMs requires a tighter, more balanced set of constraints than those imposed by traditional back-constraints. To achieve this, we developed a new form of back-constraint that is based on GP models, where we initialize this mapping by nonlinear dimension reduction methods. In addition, the shape of the trajectories in latent space is further regularized by constraining the latent space trajectories to lie on a constrained geometrical manifold (generalized elliptic or toroid manifold).
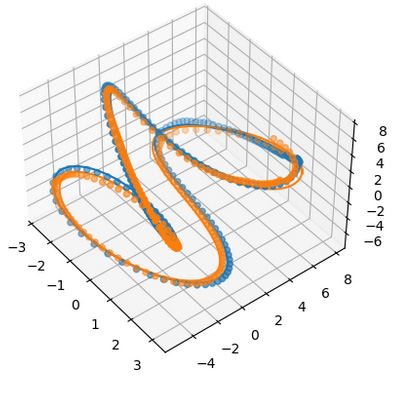 Figure 1. An example of two trajectories aligned with three dimensions of toroidal geometry included in the toroidal GP back-constraint.
Figure 1. An example of two trajectories aligned with three dimensions of toroidal geometry included in the toroidal GP back-constraint.
Inference of unobserved variables or degrees of freedom
Embedding multiple GPDMs in the same latent space results in a Bayesian probabilistic model that allows for the inference of unobserved variables using Bayesian inference methods. Specifically, this makes it possible to predict the movement over time, taking into account measured partial kinematic information, in order to determine movement class and style variables online. This makes it possible to determine an initiated action online, and to infer missing variables or to predict its further trajectory in a motion-class-specific manner.
A medical application of this framework is the modeling of bimanual actions from online measured unilateral movements in patients with unilateral impairments. Measuring the unimpaired side allows for the online synthesis of an unimpaired movement for the impaired side, which can be used to control orthotic devices. The estimation of the movement class and actual state in the latent space can be informed by the kinematics of the unimpaired side, but also additional variables such as EMG measurements. An example is the prediction of the movement of the impaired hand from the movement of the other during bimanual activities, like the opening of a jar.
Application to Data from Bimanual Activities
Inspired by activities that are highly relevant for stroke patients that use hand orthoses, we implemented the proposed solution using data from five different activities of daily living requiring bimanual coordination. The developed mixture GPDM model enables the successful embedding of all activities in the same latent space, using geometrically constrained GP back-constraints (see above). Given an initial sequence of one hand performing an action, such a model can infer the type of activity being performed. It can then employ the GPDM of the inferred action to predict the appropriate subsequent actions for coordinating the prosthesis with the healthy arm and hand with high accuracy, using less than 10 example trajectories per class for training.
 |
|
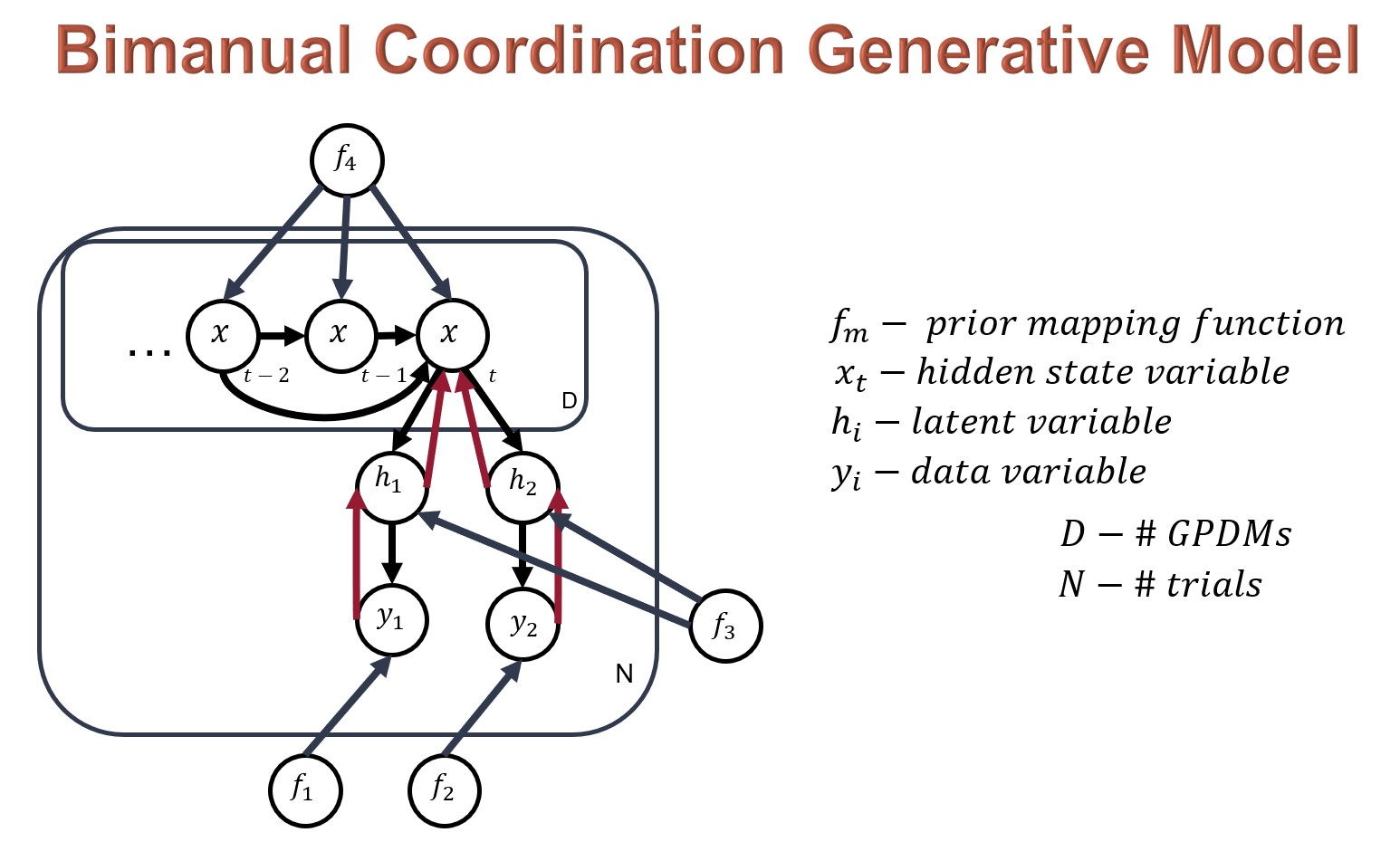
Figure 2. Model used to predict and generate movement in bimanual activities of daily living (ADLs). Information regarding the current state of the healthy arm and hand, and the impaired arm and hand enter into the model at the y_1 and y_2 data variables, respectively. Each is mapped by a gaussian process latent variable model (black arrow) to the hidden latent spaces, h_1 and h_2, regularized by back-constraints (red arrows). The hidden latent states are combined and mapped into a third latent space paired with a number of dynamical models, D, representing the total ADLs being learned in the space.
|
|
|
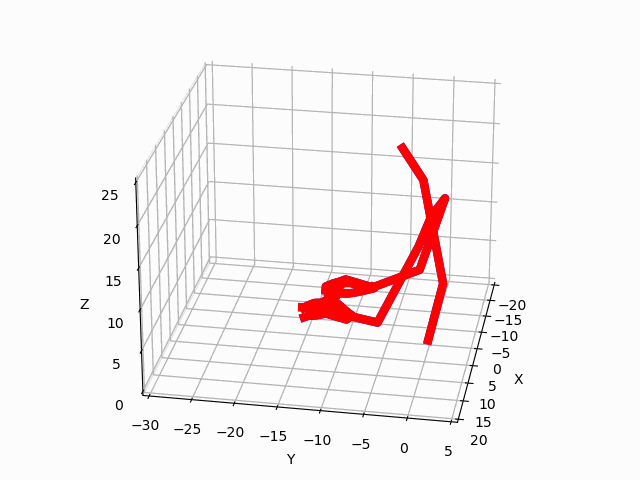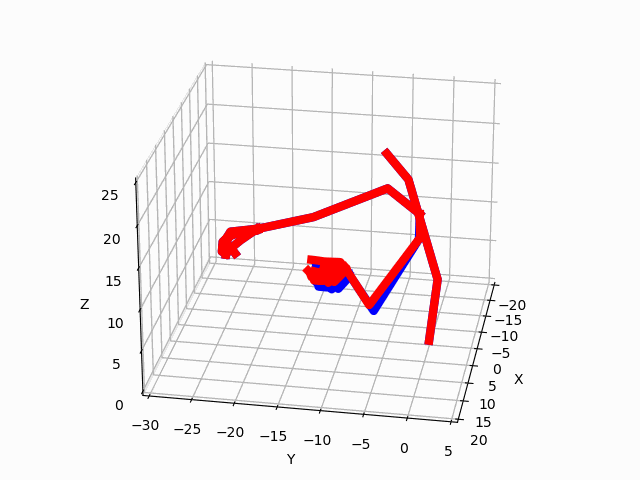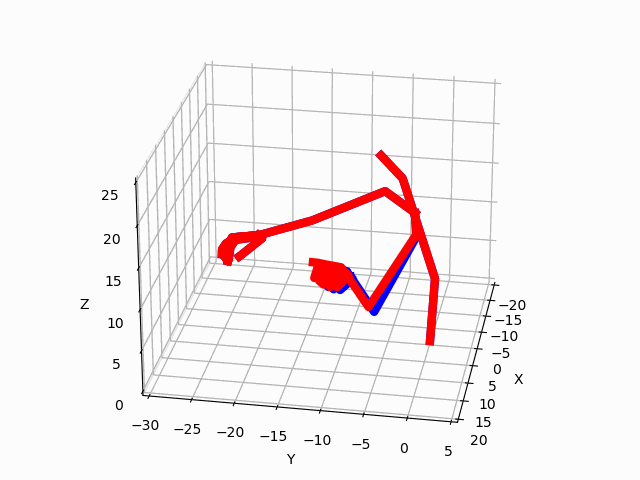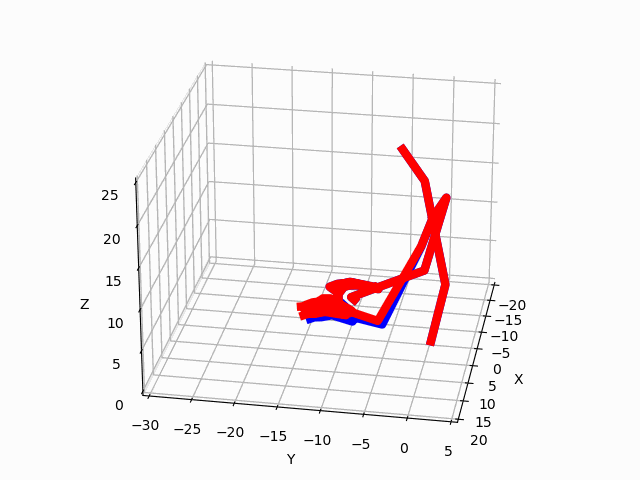 |
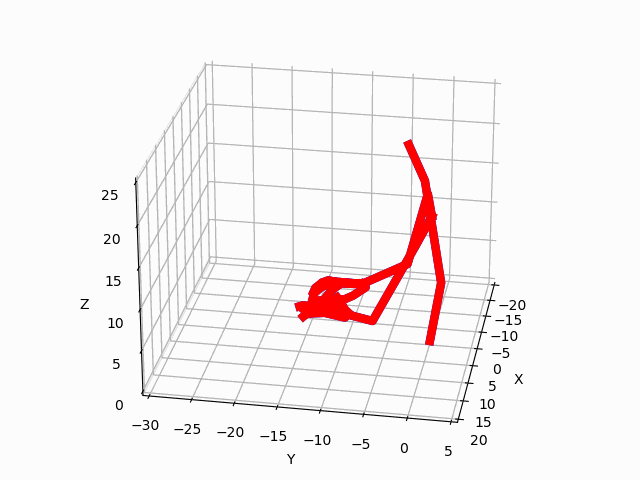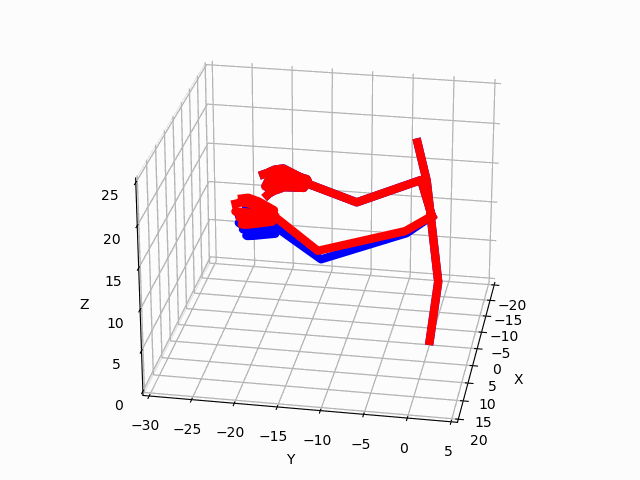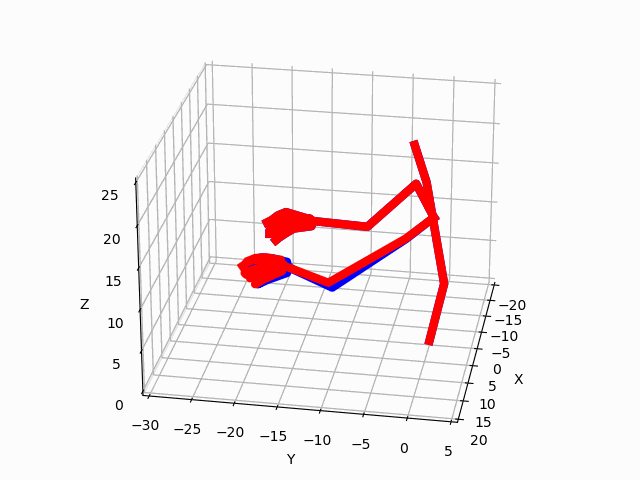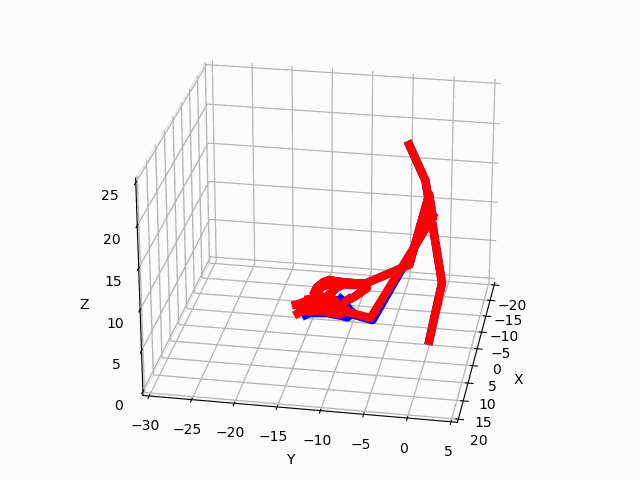
Figure 3. Predictions by our model for two ADLs. The blue avatar represents the ground truth.
The red avatar displays the generated prediction for the left hand and arm.
Prediction of Reactive Hand Kinematics from EMG
We also applied our hierarchical GP-based framework to the prediction of finger kinematics from EMG signals. This is a challenging application due to the high level of noise in such recorded biological signals, making it difficult to make predictions of complex actions at high degrees of freedom. We improved the quality of these predictions using a hierarchical GPDM that handles multiple sources of sensory information in the form of three data structures: EMG of the shoulder, upper arm, and forearm, arm kinematic data, and hand kinematic hand data. Using sparse GPLVM and GPDM approximations, we made the resulting inference architecture real-time capable. Our results demonstrate that the prediction of hand kinematics can be substantially improved by the inclusion of information from online measurements of arm kinematics, and learned models of finger kinematics.